The Geiger Counter And Counting Statistics

Caltech Senior Physics Laboratory

Experiment 2

September 1997

This experiment has three parts: the first deals with some of the physics of a Geiger-Mueller (GM) Tube and will acquaint you with some characteristics of this gas-filled detector. The second part utilizes those parts of statistical theory that apply particularly to all counting experiments. The third part examines a fundamental property of all detectors, namely the detection efficiency. This is not the simple experiment it appears to be at first glance; it contains subtleties that are not always immediately apparent. The measurement and analysis techniques encountered here are universally applicable to all other types of radiation detectors.

Introduction

A Geiger-Mueller (GM) tube is a gas-filled radiation detector. It commonly takes the form of a cylindrical outer shell (cathode) and the sealed gas-filled space with a thin central wire (the anode) held at ~ 1 KV positive voltage with respect to the cathode. The fill gas is generally argon at a pressure of less than 0.l atm plus a small quantity of a quenching vapor (whose function is described below).

If a gamma - ray interacts with the GM tube (primarily with the wall by either the Photoelectric Effect or Compton scattering) it will produce an energetic electron that may pass through the interior of the tube.

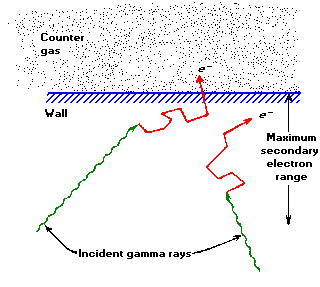
Figure 1. The principal mechanism by which gas-filled counters are sensitive to gamma- rays involves ejection of electrons from the counter wall. Only those interactions that occur within an electron range of the wall's inner surface can result in an output pulse.

Ionization along the path of the primary electron results in low energy electrons that will be accelerated towards the center wire by the strong electric field. Collisions with the fill gas produce excited states (~11.6eV) that decay with the emission of a UV photon and electron-ion pairs (~26.4 eV for argon). The new electrons, plus the original, are accelerated to produce a cascade of ionization called "gas multiplication" or a Townsend avalanche. The multiplication factor for one avalanche is typically 10⁶ to 10⁸. Photons emitted can either directly ionize gas molecules or strike the cathode wall, liberating additional electrons that quickly produce additional avalanches at sites removed from the original. Thus a dense sheath of ionization propagates along the central wire in both directions, away from the region of initial excitation, producing what is termed a Geiger-Mueller discharge.

Figure 2. The mechanism by which additional avalanches are triggered in a Geiger-Mueller discharge.

The intense electric field near the anode collects the electrons to the anode and repels the positive ions. Electron mobility is ~ 10⁴ m/s or 10⁴ times higher than that for positive ions. Electrons are collected within a few µs, while the sheath of massive positive ions (space charge) surrounding the center wire are accelerated much more slowly (ms) outward towards the cathode.

The temporary presence of a positive space charge surrounding the central anode terminates production of additional avalanches by reducing the field gradient near the center wire below the avalanche threshold. If ions reach the cathode with sufficient energy they can liberate new electrons, starting the process all over again, producing an endless continuous discharge that would render the detector useless. An early method for preventing this used external circuitry to "quench" the tube, but the introduction of organic or halogen vapors is now preferred. The complex molecule of the quenching vapor is selected to have a lower ionization potential ( < 10 eV) than that of the fill gas (26.4 eV). Upon collision with a vapor molecule the fill gas ion gives up ~ 10 eV to the quench vapor molecule which then quickly dissociates rather than losing its energy by radiative emission. The remainder of the partially neutralized vapor-atom energy (~ 4 eV) produces a UV photon that is strongly absorbed by the molecules and prevented from reaching the cathode. Any quench vapor that might be accelerated and impact the cathode dissociates on contact. Organic quench vapors, such as alcohols, are permanently altered by this process, limiting tube life to ~ 10⁹ counts. Halogen quench vapors dissociate in a reversible manner later recombining for an essentially infinite life.

Dead Time

The sheath of positive ions (space charge) close to the anode reduces the intense electric field sufficiently that approaching electrons do not gain sufficient energy to start new avalanches. The detector is then inoperative (dead) for the time required for the ion sheath to migrate outward far enough for the field gradient to recover above the avalanche threshold. The time required for recovery to a value high enough for a new pulse to be generated and counted is called the "dead time" and is of the order of 100 µs.

Measurement Of Dead Time - Two Source Method:

Measuring the dead time of a system requires two sources, S₁ and S₂ . A counting rate is measured first with S₁, then S₁ plus S₂, and finally with only S₂. If the dead time were zero the counting rate with both sources together would be simply the sum of the individual rates. The fact that it never is permits one to compute the actual dead time. At modest count rates this is straightforward. If the counting rates are very high it is necessary to decide which of two models applies, i.e., is the detector paralysable or non-paralysable.

Reference: (2) p. 96-102.

{Exercise: Work out the necessary relationship. (Assume no background.)}

Measurement Of Dead Time - Oscilloscope:

The dead time of the GM tube may be directly determined with an oscilloscope by observing the recovery envelope of the pulses. Note carefully where the CRO is connected. The test point gives information about the GM tube only. Recovery must be sufficient to produce a pulse large enough to exceed the "threshold" of the following counting circuits. The "dead time" of these circuits should also be considered.

Reference: (2) p. 225-226.

Correction Of Count Rate To Include Dead Time:

If n' counts are recorded in a time interval t with a detector of dead time d, it is necessary to compute the true number n that would have been observed with a counter of zero dead time. Since n'_d is the total dead time, and n/t is the true counting rate, (n/t)n'_d is the total number of counts that would have occurred during the total dead time interval. Therefore (n/t)n'_d = n - n'. In terms of the counting rate, R = n/t and R' = n'/t,

Pulse Size - Charge Collected:

The GM tube output is a charge pulse whose amplitude is independent of the energy of the detected radiation. The only amplitude information that it can provide is that the energy of the detected radiation was sufficient to produce electrons energetic enough to penetrate to the sensitive region of the tube. The quantity of charge produced is directly proportional to the "over voltage", i.e., the difference between the GM threshold voltage at which a GM discharge will first occur, and the higher normal operating voltage. The output signal will be directly proportional to the charge (10⁸ - 10¹⁰ ion-pairs), and inversely proportional to the circuit capacitance (GM tube capacitance + the connecting cable capacitance + the input capacitance of the electronic system). The normal signal is of the order of volts.

Counting Statistics

It is assumed that you are familiar with statistics and the definitions for sample and population means, variances, and probability distribution.

Statistics Definitions:

(From P. R. Bevington, Data Reduction and Error Analysis for the Physical Sciences, pp. 10-24.)

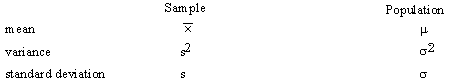
The definitions of these symbols are:

Sample Mean:

Sample Variance:

(Note the N - 1 in the definition of s² makes s² a correct estimator of sigma².)

Poisson Distribution:

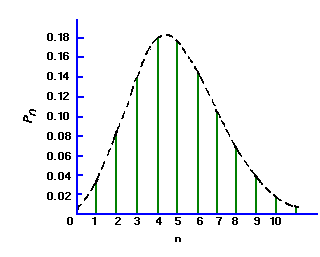
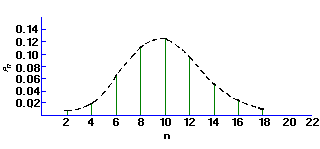
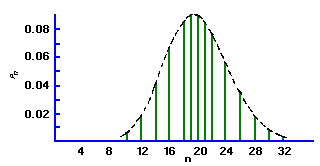
Under the conditions that are thought to apply to all radioactive decays (i.e., all the nuclei are identical, independent, and each has a definite and constant probability of decay in a unit time interval), one can derive a distribution function P(x) that is the probability of observing x counts in one observation period.

The distribution of the values x about the true average µ is called the Poisson distribution and has the form:

(2)

{Exercise: Show that for the Poisson distribution, s² equals the mean value µ.}

References: (1) p. 750-753 (3) p. 34-35 (4) p. 36-42

The Meaning Of Sigma:

If the mean of a Poisson distribution becomes ~20, the distribution becomes symmetrical, assuming the characteristics of a Normal, or bell-shaped Gaussian distribution. This displays the characteristic that 68% of the total area of the distribution lies within ± sigma of the mean. For a Poisson distribution sigma=sqrt(µ) , so that a counting measurement is 68% likely to be within ± sigma of the true population mean µ Since x is probably close to µ, we may take sigma = sqrt(x), and say that a single measurement is 68% likely to be within ± sqrt(x) of the true mean. Similarly the values for ± 2 sigma and ± 3 sigma are 95% and 99.7%, respectively. When plotting experimental results, it is customary to include error bars of length sigma₁ on each point x_i.

Propagation Of Errors:

Often a desired value is a function of several measured values each of which has finite statistical uncertainties. If a value Z = f (X,Y) is a function of independent random variables X and Y, there will be a certain spread in Z associated with spreads in the values of X and Y. By using probability theory it is not difficult to derive the following general formula:

which relates the expected uncertainty in a calculation of Z to the corresponding uncertainties, sigma_x and sigma_y , of X and Y. Both the random variables X and Y must have a normal distribution, with the uncertainties in both X and Y small enough so that the differentials accurately describe the variations in Z. Note also that Poisson random variables are nearly normal when m > 20, so that this formula usually will hold quite well.

{Exercise: Express the uncertainty in X+Y, X-Y, XY, X/Y, and ln(X) in terms of s_x and of s_y. Write the uncertainties in XY and X/Y to show the fractional uncertainty in terms of the fractional uncertainties in X and Y. Do you see the mnemonic value of this?}

References: (1) p. 768-769, (4) Chap. 4, (3) p. 51-55.

Experimental Tasks

The apparatus consists of a halogen quenched Geiger-Mueller tube (TGM Model N106/3P) that may be used in or out of a lead shielded "house", a Counter/Timer/High-voltage Power Supply (Nucleus Model 550), and various radioactive sources. Be certain you understand the correct procedures for handling radioactive sources. See the Primer On The Effects Of Exposure To Ionizing Radiationthat also contains an inventory of the radioactive sources available in the laboratory.

1: Finding the best operating point for the GM tube.

Apply 500V to the tube with a moderate strength ¹³⁷Cs source (50 µCi) nearby. Increase the HV until counts begin to appear, then record the count rate as a function of voltage for a few points up to ll00 V. Do you see the end of the flat region of counts vs. voltage? This flat region is called the plateau. DO NOT EXCEED ll00 V AT ANY TIME, as this will cause a continuous arc that destroys the tube by permanently dissociating the quenching gas. Estimate (just roughly) the %/V slope of the count rate curve near the middle of the plateau. Formerly this slope was important because HV power supplies were much less stable than they are today. Set an operating point that is near the middle of the plateau for your measurements.

2. Measuring the dead time. (Two source and CRO Method)

A high count rate is required to produce a significant dead time and to achieve sufficiently small statistical uncertainties in a reasonable time, as well as produce a usably visible CRO trace. Use one of the 250 µCi ¹³⁷Cs sources. Observe the dead time directly on the CRO by attaching a l0x probe to one of the 550 connectors labeled "COUNTS". Consult the 550 circuit diagram for details.

A vertical sensitivity of 2 V/div and a sweep speed of about 20 µs/div are suggested. When measuring a dead time from the recovery envelope be aware that the counting circuits contain a threshold discriminator (See 550 Manual).

When you attach anything to the "COUNTS" connector, what is done to the capacitance that must be charged by the GM tube? Attach a cable (48-60 inch RG-58/U, 30 pF/ft) to the second "COUNTS" connector. Compare the signal amplitude with and without the cable attached. Why use a l0x probe to make the connection rather than a coax cable? How much charge is contained in a full amplitude pulse? Can you estimate the total capacitance that the GM tube must charge up to produce its output pulses?

Use two similar strong sources (each 250 µCi). It is best to secure the GM tube to a thick bed of plastic foam to minimize any scattering from nearby material. Place Source 1 at the midpoint of the bare detector very nearly touching it. Take a counting run and measure the dead time on the CRO. Place Source 2 similarly on the other side of the tube, count and measure this dead time on the CRO. Remove Source 1, count and measure this dead time with the CRO. Count for times long enough for statistical uncertainties in N₁, N_l+N₂, and N₂ that are small compared to the differences (N_l+N₂) - N_l, etc.

Calculate the dead time. Compare your CRO data to the corresponding counting data. Are they consistent? Explain any differences. What is the approximate uncertainty in the calculated dead time? Is this detector paralysable, or non-paralysable? Explain. (Reference (2), p.96-102.)

3. Examining a Poisson Distribution.

Use only "natural room background" radiation as a source with the GM tube in its lead "house". Take 0.5 minute runs and plot them on a histogram until the shape of the distribution emerges, or you have 20 runs. Counting at low rates for short time intervals (x < 20) produces the characteristically skewed Poisson distribution.. Now calculate x-bar and s. How well does s match with sqrt(x) ? How many of the points fall within ± s of x-bar? What is the source of the background?

Reference (2) p. 774-780

4. GM Tube Detection Efficiency.

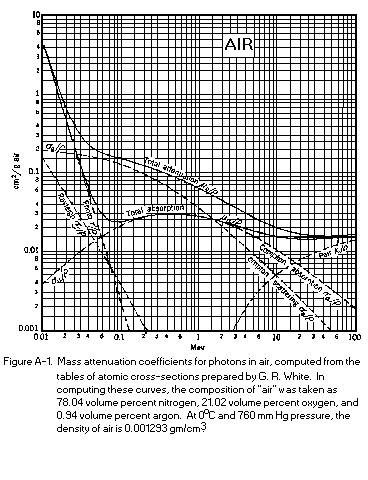
Estimate the efficiency of the GM tube using the attached plot of the total mass attenuation coefficient for aluminum and the energy of a ¹³⁷Cs gamma ray. Assume that the walls of the tube are thin enough so that any interaction that will scatter an electron in the proper direction will produce a count. Should you use the absorption or the attenuation coefficient? (see Evans, p. 686-689) Is the air between source and detector important? Is the mass attenuation coefficient for air comparable to that for aluminum? Consider the shape of the wall(s) of the tube. (See SUGGESTION below.)

Relevant parameters are: Wall = 30 mg/cm² Aluminum, Fill Gas = Argon 95%/Halogen Quenching Vapor 5%, Total fill pressure ~5 cm Hg, Density of air ~1.3 mg/cm³

Now measure the efficiency. (SUGGESTION: Use the bare tube on a foam platform with as large a separation between the source and detector as permits a reasonable count rate.) Consider the effects of "background". To calculate the total emission from the source you will need an understanding of the ¹³⁷Cs decay scheme (See "'Internal Conversion", in any of References 1-3), the strength of the source, its half - life, and the calibration date. (Data on last page of the Primer On The Effects Of Exposure To Ionizing Radiation ) How well do the calculated and measured values agree? The decay schemes of several frequently used sources are provided in Appendix . See also the Guide to the TABLE OF ISOTOPES. Would a correction for the shape of the wall be significant?

Questions

{Be sure to do exercises 1, 2, and 3 in the text.}

1. Is it possible for a gamma - ray to interact with a free electron by means of the Photoelectric Effect?

2. How does the avalanche phenomenon differ from gas multiplication?

3. Which is more important in producing a signal - the collection of electrons at the anode or the less rapid increase in the diameter of the positive ion sheath?

4. Which is more important in the operation of a Geiger tube - a large total potential drop or a large electric field gradient? What does the radial variation in electric field look like?

5. Given a counter with a plateau threshold of 975 V, what changes in the design of the counter should be made to lower that threshold?

6. How does the efficiency of a Geiger counter vary with photon energy? How does the choice of wall material and thickness affect the efficiency? How could you increase the efficiency of the GM tube that you used, without the use of any tools?

References

1. * R. D, Evans, The Atomic Nucleus, McGraw Hill Book Company.

2. * G. Knoll, Radiation Detection And Measurement, McGraw Hill Book Company, 1989.

3. * N. Tsoulfanidis, Measurement And Detection Of Radiation, McGraw Hill Book Company, 1995.

4. * C. M. Lederer and V. S. Shirley, Table Of Isotopes, 6th Edition, 1967; 7th Edition, 1978; or R. B. Firestone and V. S. Shirley 8th Edition, 1996, Wiley - Interscience.

5. * P. Bevington, D. K. Robinson, Data Reduction And Error Analysis For The Physical Sciences, McGraw-Hill Book Company, 1992.

6. S. A. Korff, Electron And Nuclear Counters, Van Nostrand Co.

7. W. Price, Nuclear Radiation Detection, McGraw Hill Book Company, 1964.

8. E. Bleuler and G. Goldsmith, Experimental Nucleonics, Holt, Rinehart and Winston.

All of these are available in the lab. References with * are considered primary references.

Appendix A